Op het eerste gezicht lijkt alles eenvoudig: een raster, een paar lijnen en het antwoord lijkt voor de hand te liggen. Toch trappen we vaak in een valkuil. Waarom? Omdat onze hersenen beelden controleren, vereenvoudigen en verborgen details weglaten. In gevallen waarin we te snel hebben gehandeld, is alles al gebeurd. Wat als de sleutel tot tijdelijke verlichting is dat er een andere, passende aanpak is, een die is overgenomen door logica?
Waarom geven deze rasters ons dit?
Foto
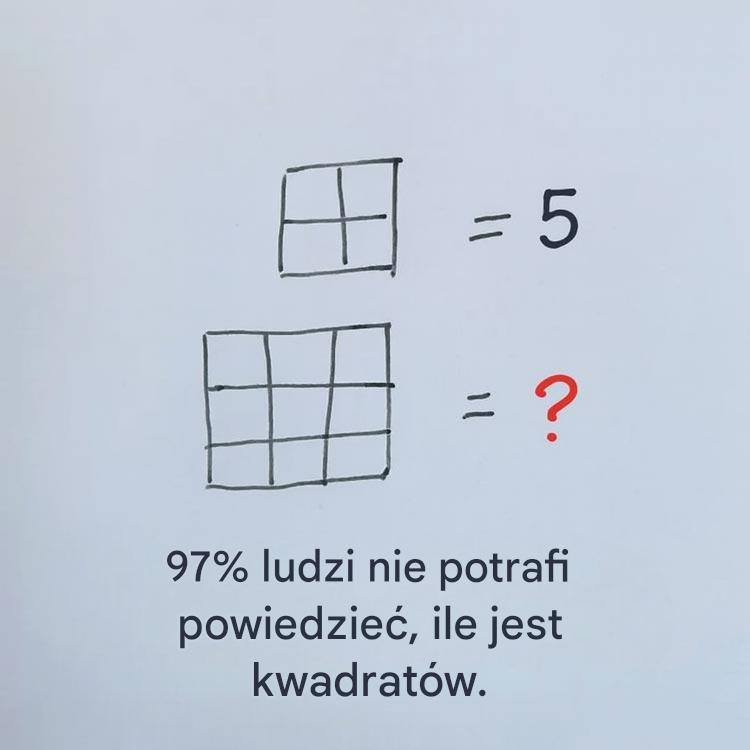
Het probleem is als een logisch spel: je raakt enthousiast en ontdekt dan dat het er veel meer heeft. Een 3×3 raster bestaat bijvoorbeeld niet alleen uit kleine, opvallende vierkanten. Het bevat ook discrete combinaties: kleine vierkanten bestaande uit 2×2 vierkanten en grote vierkante gehelen. Als je niet aan deze eenheden denkt, mis je het verhaal. Het goede nieuws is: er is een eenvoudige manier om alles te evalueren zonder iets weg te laten.
Stapsgewijze methode voor het berekenen van vierkanten
De meest voor de hand liggende: vierkanten ter grootte van een enkel nest. In een 3×3 raster zijn er 9 (één per vakje). Naast de 2×2 vierkanten zijn er kleinere vierkanten. Hoeveel passen er in? Stel je voor dat je een 2×2 vierkant in het raster sleept: het kan beginnen in de linkerbovenhoek, middenboven, links van het midden, enz. Er zijn er in totaal 4. Voeg ten slotte een enorm vierkant toe dat het hele raster beslaat: 1. Dus we krijgen 9 + 4 + 1 = 14. Klaar! Niet de andere vergrootglazen, gewoon een kleine variant.
Een geheugensteuntje dat alles verandert
Advertentie